命題1
2つの等しくない数が提示され、小さい数が絶えず大きい数から引かれるとき、単位が残されるまで、残された数がその前の数を割り切らないならば、最初の数は互いに素である。
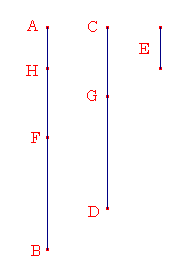
2つの等しくない数ABとCDの小さい数は絶えず大きい数から引かれて、単位が残されるまで残された数はその前の数を割り切らないとする。
ABとCDが互いに素であることを言う。つまり、単位のみがABとCDを割り切る。definitionⅦ.12
ABとCDが互いに素でないならば、ある数Eがそれらを割り切る。CDを、BFを割り切り、それ自身より少ないFAを残すとし、AFを、DGを割り切り、それ自身より少ないGCを残すとし、そしてGCを、FHを割り切り、単位HAを残すとする。
EはCDを割り切り、そしてCDはBFを割り切るから、それゆえにEもまたBFを割り切る。
しかしそれはまた全体BAを割り切り、それゆえにそれは余りAFを割り切る。しかしAFはDGを割り切り、それゆえにEもまたDGを割り切る。しかしそれはまた全体DCを割り切り、それゆえにそれはまた余りCGを割り切る。
しかしCGはFHを割り切り、それゆえにEもまたFHを割り切る。しかしそれはまた全体FAを割り切り、それゆえに、不可能であるけれども、それは余りである単位AHを割り切る。
それゆえに数ABとCDを割り切る数はない。それゆえにABとCDは互いに素である。definitionⅦ.12
それゆえに、2つの等しくない数が提示され、小さい数が絶えず大きい数から引かれるとき、単位が残されるまで、残された数がその前の数を割り切らないならば、最初の数は互いに素である。
証明終了